
Alternatively if you want to be able to truly understand how to train a neural network, read at your own peril.įirst, a vector can be seen as a list of numbers, and a matrix can be seen as an ordered list of vectors. If the Jacobian from yesterday was spooky enough already, I recommend reading no further. In order to work with neural networks, we need to introduce the generalized Jacobian. However, in order to truly understand backpropagation, we must go beyond mere Jacobians. Not only do we have an intuitive understanding of the Jacobian, we can now formulate the vector chain rule using a compact notation - one that matches the single variable case perfectly. Our understanding of Jacobians has now well paid off. It turns out, that for a function f : R n → R m and g : R k → R n, the chain rule can be written as ∂ ∂ x f ( g ( x ) ) = ∂ f ∂ g ∂ g ∂ x where ∂ f ∂ g is the Jacobian of f with respect to g. This way it is intuitively clear that we can cancel the fractions on the bottom, and this reduces to d f d x, as desired. Alternatively we can write the rule in a way that makes it more obvious what we are doing: d d x f ( g ( x ) ) = d f d g d g d x, where g is meant as shorthand for g ( x ). But if we write it this way, then it's in an opaque notation and hides which variables we are taking the derivative with respect to. This is simply d d x f ( g ( x ) ) = f ′ ( g ( x ) ) g ′ ( x ).

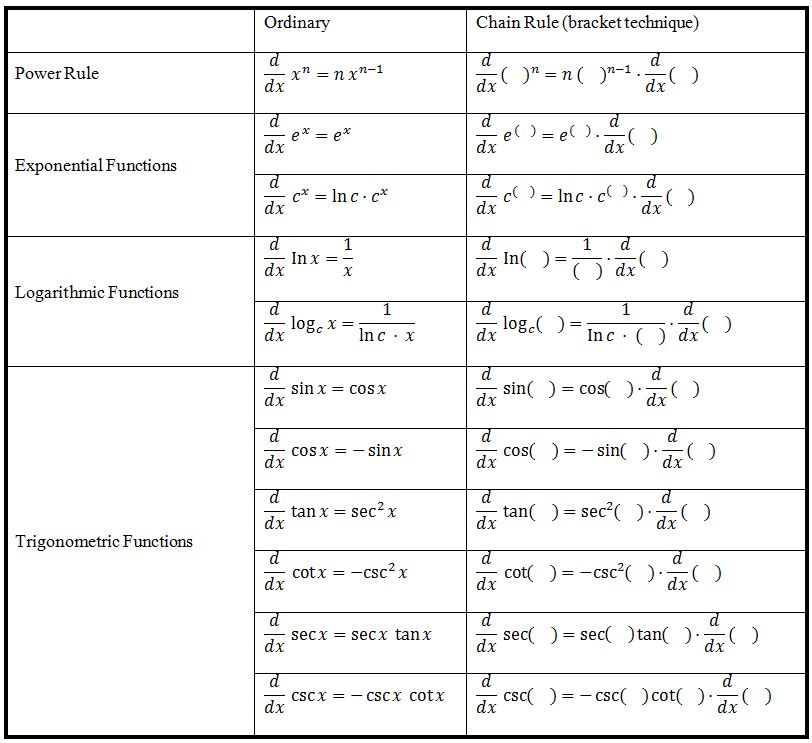
We start by describing the single variable chain rule.

Unfortunately, the notation can get a bit difficult to deal with (and was a pain to write out in Latex). What I have discovered is that, despite my initial fear of backpropagation, it is actually pretty simple to follow if you just understand the notation. 1 Plus, if we were writing our own library, we'd want to know what's happening in the background. However, while this might be great for practitioners of deep learning, here we primarily want to understand the notation as it would be written on paper. These days, modern deep learning libraries provide tools for automatic differentiation, which allow the computer to automatically perform this calculus in the background. However, backpropagation is notoriously a pain to deal with. That's where the backpropagation enters the picture.īackpropagation is simply a technique to train neural networks by efficiently using the chain rule to calculate the partial derivatives of each parameter. What's hard is making the whole thing efficient so that we can get our neural networks to actually train on real world data. The learning part refers to the fact that we are allowing the properties of the function to be set automatically via an iterative process like gradient descent.Ĭonceptually, combining these two parts is easy. In other words, in order to perform a task, we are mapping some input x to an output y using some long nested expression, like y = f 1 ( f 2 ( f 3 ( x ) ) ). The deep part refers to the fact that we are composing simple functions to form a complex function. I initially planned to include Hessians, but perhaps for that we will have to wait.ĭeep learning has two parts: deep and learning. Here, I will focus on an exploration of the chain rule as it's used for training neural networks. This post concludes the subsequence on matrix calculus.


 0 kommentar(er)
0 kommentar(er)
